Technieken voor het multivariaat beantwoorden van een onderzoeksvraag

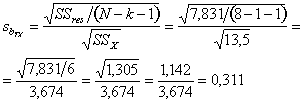
Inhoud:
Tweewegs-variantieanalyse
Meervoudige regressieanalyse

Tweewegs-variantieanalyse en meerwegs-variantieanalyse

Met deze toets ga je na of twee (of meer) groepsindelingen afzonderlijk en gezamenlijk effect hebben op de gemiddelde score van eenheden (respondenten) op een kwantitatieve variabele. De indeling in groepen gebeurt met twee (of meer) onafhankelijke variabelen: de twee (of meer) factoren in deze variantieanalyse. De groepen op elk van beide factoren worden ook factorniveaus genoemd.

Statistische nulhypothesen

• Voor elk hoofdeffect is er de statistische nulhypothese dat de groepen op deze variabele gelijke populatiegemiddelden hebben. Maak in de omschrijving van de groepen duidelijk om welke onafhankelijke variabele (factor) het gaat. Je hoeft maximaal drie groepen expliciet te noemen.
  Voorbeeld: verschillen tussen kranten. H₀: μ_NRC = μ_Volkskrant = ... = μ_{overige kranten}.
  NB '...' staat hier voor alle overige kranten.
• Voor elk interactie-effect is er de statistische nulhypothese dat de subgroepen op de gecombineerde factoren gelijke populatiegemiddelden hebben. Maak in de omschrijving van de subgroepen weer duidelijk om welke onafhankelijke variabelen (factoren) het gaat. Je hoeft maximaal drie subgroepen expliciet te noemen.
  Voorbeeld: verschillen tussen kranten in combinatie met geslacht. H₀: μ_NRC*vrouw = μ_NRC*man = ... = μ_{overige kranten*man}.

Voorwaarden

Het boek van Van Peet et al. specificeert 5 voorwaarden, waarvan er in de praktijk drie belangrijk zijn:

1. De afhankelijke variabele moet minstens op interval niveau gemeten zijn.
2. De groepen kunnen beschouwd worden als onafhankelijke steekproeven.
   Variantieanalyse voor gepaarde waarnemingen bestaan ook, maar we behandelen dit niet in het vak IS.
3. De groepen hebben gelijke varianties voor de afhankelijke variabele in de populatie.
   Deze voorwaarde is alleen belangrijk wanneer de groepen niet ongeveer even groot zijn. SPSS rapporteert Levene's Test of Equality of Error Variances waarmee je kunt controleren of je van gelijke populatievarianties mag uitgaan.

SPSS commando

• Om een variantieanalyse uit te voeren met twee of meer onafhankelijke variabelen, kies je: ANALYZE-GENERAL LINEAR MODEL-UNIVARIATE.
• Het menu bevat een keur aan mogelijkheden om een model te specificeren. De meeste van deze opties vereisen meer kennis van analysemethoden dan we in deze cursus leren.
  Voor het uitvoeren van variantieanalyse met meer dan één categorische onafhankelijke variabele en één afhankelijke (die minimaal op intervalniveau gemeten is), doe je het volgende. Je selecteert de interval variabele waarvan je de groepsgemiddelden wilt vergelijken voor verschillende groepen respondenten. Deze zet je in het vakje Dependent Variable. Selecteer vervolgens de variabelen die de groepen definiëren waarvan je de gemiddelden wilt vergelijken. Deze zet je in het vakje Fixed Factor(s).
• Het is handig om onder de button OPTIONS ‘Descriptive Statistics’ aan te vinken, zodat je de groepsgemiddelden en hun standaarddeviaties krijgt.
  Kies hier ook de optie 'Homogeneity tests' om Levene's toets op homogene varianties te laten uitvoeren.
  In tegenstelling tot Van Peet et al. gebruiken we de partiële η² niet als maat voor de effectgrootte. Vink dus de optie Estimates of effect size NIET aan. Deze maat is omstreden: een hoofdeffect heeft in een eenwegs-variantieanalyse bijvoorbeeld een andere partiële η² dan in een tweewegs-variantieanalyse ook al blijft de tussengroepen en totale kwadratensom exact gelijk. In plaats daarvan gebruiken we de gewone η², die je echter met de hand moet uitrekenen.
• Als je twee onafhankelijke variabelen selecteert, wordt automatisch een analyse uitgevoerd met de hoofdeffecten van beide variabelen en het interactie-effect.
  Via de button MODEL kun je dit desgewenst wijzigen, bijvoorbeeld het interactie-effect weglaten. Kies bij Model voor Custom, selecteer 'Main effects' onder Build Term(s) Type, selecteer de onafhankelijke variabelen in het linker lijstje waarvoor je de hoofdeffecten wilt laten schatten en kopieer ze met de pijl-knop naar de rechter lijst.
  Interactie-effecten kun je samenstellen door twee onafhankelijke variabelen in het linker lijstje te selecteren, Interaction te kiezen onder Build Term(s) Type en vervolgens op de pijl-knop te klikken. Wanneer je meer dan twee onafhankelijke variabelen selecteert in het linker lijstje, krijg je een interactie-effect van meer dan twee variabelen.
  Bij een variantieanalyse met meer dan twee factoren is het handig om interactie-effecten van meer dan twee variabelen uit het model weg te laten via Custom.
• Laat de optie 'Type III' staan achter 'Sum of Squares' en laat de optie ‘Include intercept in model’ aangevinkt staan in het MODEL dialoogscherm.
• Klik op de knop POST HOC. Als je wilt weten welke gemiddelden significant van elkaar verschillen en welke niet, dan gebruik je deze optie. Er zijn meerdere post-hoc toetsen beschikbaar, waaronder die van Bonferroni.
  Op deze manier krijg je alleen paarsgewijze vergelijkingen voor de hoofdeffecten. Wanneer je die ook wilt krijgen voor het interactie-effect, moet je in de syntax file de volgende regel toevoegen onder de /POSTHOC regel: /EMMEANS=TABLES(factor_A BY factor_B) COMPARE(factor_B) ADJ(BONFERRONI)
  De meervoudige vergelijkingen voor het interactie-effect vormen geen verplichte stof binnen het vak IS.
  Vul op de plaats van factor_A de naam van de variabele in die als eerste factor gebruikt wordt en op de plaats van factor_B de naam van de variabele die de tweede factor voorstelt.
• Lijngrafiekjes die de verschillen tussen de groepen laten zien, kun je krijgen via PLOTS. Zet de categorische variabele die je als factor gebruikt in het vakje onder ‘Horizontal axis’ en druk op ‘Add’ om straks een grafiekje te krijgen dat het hoofdeffect van deze factor weergeeft. Een grafiek met het interactie-effect van twee factoren krijg je door een van beide categorische variabelen in het vakje onder ‘Horizontal Axis’ te zetten en de andere in het vakje onder ‘Separate lines’.

SPSS Output

De belangrijkste output van SPSS is weer de samenvattende tabel, die nu Tests of Between-Subjects Effects heet. In deze tabel zijn de voor ons belangrijke rijen geel gemarkeerd.

Tests of Between-Subjects Effects
Dependent Variable:na Houding t.a.v. roken na reclamecampagne
Source	Type III Sum of Squares	df	Mean Square	F	Sig.
Corrected Model	127,279a	5	25,456	17,483	,000
Intercept	298,050	1	298,050	204,705	,000
Sekse	,869	1	,869	,597	,442
behandeling2	90,966	2	45,483	31,238	,000
Sekse * behandeling2	33,723	2	16,861	11,581	,000
Error	135,408	93	1,456
Total	565,000	99
Corrected Total	262,687	98
a. R Squared = ,485 (Adjusted R Squared = ,457)

Deze tabel geeft:

• De kwadratensom (Sum of Squares) die hoort bij de verschillen tussen de groepen op elk van de hoofdeffecten (hier: behandeling en sekse) en voor het interactie-effect (hier: sekse * behandeling). Hoe groter de kwadratensom, des te groter zijn de verschillen tussen de gemiddelden van de groepen.
• De kwadratensom binnen de groepen (Error), die aangeeft hoeveel ‘foute’ of toevallige verschillen er zijn.
• De gecorrigeerde totale kwadratensom (Corrected Total). Dit is ongeveer het totaal van de kwadratensommen tussen en binnen de groepen, maar niet precies hetzelfde.
  Bij de berekening van de kwadratensommen die hier gebruikt wordt (Type III), wordt apart een kwadratensom uitgerekend voor het hele model, dat wil zeggen voor alle hoofdeffecten en interactie-effecten samen. De kwadratensom van dit gecorrigeerde model (Corrected Model) vormt samen met de kwadratensom van de fouten (verschillen binnen de groepen) de gecorrigeerde totale kwadratensom. De gecorrigeerde totale kwadratensom heeft wel het aantal vrijheidsgraden dat we gewend zijn: N - 1.
• Er is ook nog een kwadratensom voor het intercept (het gemiddelde over alle waarnemingen), waar we alleen naar kijken wanneer we willen toetsen of dit totaalgemiddelde in de populatie nul is. Meestal is dit geen interessante hypothese.
• Tenslotte is er een (tweede) totale kwadratensom (Total), maar daar kijken we verder niet naar. Let op, deze totale kwadratensom heeft een afwijkend aantal vrijheidsgraden: N in plaats van N - 1.
• De kwadratensommen van de hoofdeffecten, de interactie-effecten en de verschillen binnen de groepen worden door hun vrijheidsgraden (df) gedeeld om het gemiddelde kwadraat te krijgen (Mean Square).
• De toetsingsgrootheid F is gelijk aan de gemiddelde kwadratensom tussen de groepen gedeeld door de gemiddelde kwadratensom binnen de groepen. Deze F toetst de nulhypothese dat alle groepsgemiddelden gelijk zijn (dat hun verschil nul is). We hebben dus voor elk (hoofd- en interactie)effect een F waarde.
• De overschrijdingskans van deze toets staat onder Sig.. Een significant resultaat betekent hier dat de nulhypothese verworpen moet worden, dus dat er wel verschillen zijn tussen de groepsgemiddelden.

Wanneer een post-hoc toets met Bonferroni correctie is opgevraagd, worden de vergelijkingen tussen alle paren van gemiddelden getoond. Aangezien deze toets alleen op hoofdeffecten wordt uitgevoerd, kan zij precies zo geïnterpreteerd worden als bij de eenwegs-variantieanalyse (zie daar).

Wanneer Descriptive Statistics zijn opgevraagd, wordt onderstaande tabel getoond. Hierin worden de proefpersonen eerst uitgesplitst naar de eerste factor en vervolgens naar de tweede factor. We vinden het gemiddelde, de standaarddeviatie en het aantal waarnemingen (N) dus eerst voor de mannen die de voorlichtingscampagne niet hebben gezien, dan voor de mannen die de campagne soms zagen, daarna voor de mannen die de campagne vaak zagen en tenslotte voor alle mannen. Vervolgens wordt dit herhaald voor de vrouwen.
Om de gemiddelden te vinden die horen bij het hoofdeffect ‘campagne gezien’, moet je de drie gemiddelden vergelijken in de rij 'Total' onderaan de tabel. Om het gemiddelde van alle mannen te vergelijken met het gemiddelde van alle vrouwen, moet je in de rij 'Total' kijken bij 'man' en bij 'vrouw'. Deze twee gemiddelden (-1,63 en -1,86) tonen de aard van het hoofdeffect van de factor sekse.

Descriptive Statistics
Dependent Variable:na Houding t.a.v. roken na reclamecampagne
Sekse	behandeling2 Voorlichtingscampagne gezien	Mean	Std. Deviation	N
,00 man	1,00 nee	-1,1765	,88284	17
	2,00 soms	-1,6250	1,14746	16
	3,00 vaak	-2,1250	1,40831	16
	Total	-1,6327	1,20232	49
1,00 vrouw	1,00 nee	-,3125	,94648	16
	2,00 soms	-1,2353	1,25147	17
	3,00 vaak	-3,9412	1,47778	17
	Total	-1,8600	1,97959	50
Total	1,00 nee	-,7576	1,00095	33
	2,00 soms	-1,4242	1,19975	33
	3,00 vaak	-3,0606	1,69447	33
	Total	-1,7475	1,63722	99

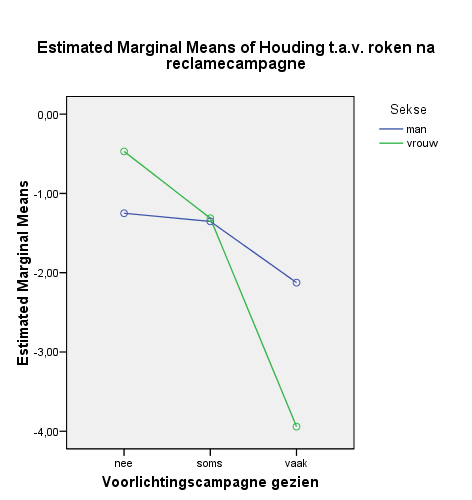
Om de aard van het interactie-effect te beschrijven, zou je alle zes gemiddelden moeten vergelijken van de subgroepen: ‘nee/man’, ‘nee/vrouw’, ‘soms/man’ … ‘vaak/vrouw’. Dat valt niet mee in een tabel. Daarom is een lijngrafiek van die (geschatte) gemiddelden inzichtelijker. Deze grafiek krijg je wanneer je het commando daarvoor hebt gegeven bij PLOTS. In onderstaand voorbeeld zien we dat bij vrouwen de houding t.a.v. roken veel lager is wanneer zij de campagne vaak zagen dan bij mannen. De houding t.a.v. roken daalt bij de vrouwen veel sterker naarmate ze de campagne regelmatiger zagen dan bij de mannen.

Wanneer je via de syntax ook de paarsgewijze vergelijkingen voor het interactie-effect hebt opgevraagd, krijg je (onder andere) ook onderstaande tabel in de output.
Hier wordt binnen elke voorlichtingsgroep (niet, soms, vaak de voorlichting gezien) een paarsgewijze vergelijking gemaakt tussen mannen en vrouwen. We zien dat binnen de respondenten die de voorlichtingscampagne niet gezien hebben, de mannen significant lager scoren op de rookhouding dan de vrouwen, M_verschil = -0,86, p = 0,043, maar dat zij juist significant hoger scoren dan de vrouwen binnen de groep die de voorlichtingscampagne vaak heeft gezien, M_verschil = 1,82, p < 0,001. Zoals de grafiek al liet zien: bij mannen maakt het vaker zien van de campagne weinig verschil terwijl dit bij vrouwen wel veel verschil uitmaakt voor de houding ten aanzien van roken.

Pairwise Comparisons
Dependent Variable:na Houding t.a.v. roken na reclamecampagne
Voorlichtingscampagne gezien	(I) Sekse	(J) Sekse	Mean Difference (I-J)	Std. Error	Sig.a	95% Confidence Interval for Differencea
						Lower Bound	Upper Bound
1,00 nee	,00 man	1,00 vrouw	-,864*	,420	,043	-1,699	-,029
	1,00 vrouw	,00 man	,864*	,420	,043	,029	1,699
2,00 soms	,00 man	1,00 vrouw	-,390	,420	,356	-1,224	,445
	1,00 vrouw	,00 man	,390	,420	,356	-,445	1,224
3,00 vaak	,00 man	1,00 vrouw	1,816*	,420	,000	,982	2,651
	1,00 vrouw	,00 man	-1,816*	,420	,000	-2,651	-,982
Based on estimated marginal means
*. The mean difference is significant at the ,05 level.
a. Adjustment for multiple comparisons: Bonferroni.

Rapportage

Vermeld het volgende:

• Vermeld het soort variantieanalyse dat je hebt uitgevoerd. Hier is dat de tweewegs-variantieanalyse.
• De samenvattende tabel met de resultaten van de variantieanalyse (de kwadratensommen, vrijheidsgraden, gemiddelde kwadraten, F-waarde en de overschrijdingskans) hoeft niet getoond te worden maar is wel overzichtelijk bij een tweewegs- en meerwegs-variantieanalyse. Wanneer je deze tabel NIET toont, moet je het toetsresultaat voor elk effect vermelden in de interpreterende tekst: F (df₁, df₁) en p. Let op, je vermeldt twee vrijheidsgraden: eerst die van de teller (tussen groepen), dan die van de noemer (binnen groepen, fouten).
• Als een effect significant is, vermeld en interpreteer je ook eta² (of met de Griekse letter: η²).
• Vermeld bij elk significant effect de gemiddelde scores van de groepen met de standaarddeviaties (in een tabel of in de interpreterende tekst) en maak duidelijk wat de eenheden en variabelen in het onderzoek zijn.
• Wanneer een post-hoc Bonferroni-toets is uitgevoerd, vermeld je tussen welke groepsgemiddelden er significante verschillen gevonden zijn. Vermeld zowel het gemiddelde verschil (M_verschil) als de bijbehorende overschrijdingskans (p).
• Wanneer de groepen niet ongeveer even groot zijn, vermeld je het resultaat van de test op homogeniteit van varianties (Equal Error Variances): F (df₁, df₁) en p.

Rekenen voor reguliere studenten

Net als bij eenwegs-variantieanalyse moet je een samenvattende tabel verder kunnen invullen wanneer de kwadratensommen zijn gegeven. De vrijheidsgraden moet je kunnen afleiden uit informatie over de omvang van de steekproef (N) en het aantal groepen (factorniveaus) dat vergeleken wordt per factor. Vervolgens moet je de gemiddelde kwadratensommen kunnen berekenen en daarmee de waarde van de toetsingsgrootheid F voor elk hoofdeffect en interactie-effect. Je kunt uit de formules op het formuleblad afleiden hoe je dit moet doen. De overschrijdingskans hoef je niet uit te rekenen maar je moet wel kunnen nagaan of het resultaat significant is op 5% met behulp van de significantietabellen.
Verder moet je eta kwadraat kunnen uitrekenen voor elk effect. Deel de kwadratensom van het effect steeds door de (corrected) totale kwadratensom. Met de formules van het formuleblad werkt dit als volgt.
De twee hoofdeffecten van factoren A en B:

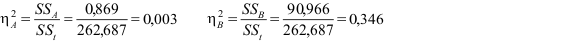
Eta kwadraat voor het interactie-effect:

Rekenen voor excellentiegroep

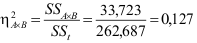
In deze groep moet je ook met de hand een tweewegs-variantieanalyse volledig kunnen uitrekenen. De gang van zaken is vergelijkbaar met die van een eenwegs-variantieanalyse, alleen het aantal stappen neemt toe. Dit geldt overigens alleen wanneer de groepen binnen elke factor en combinatie van factoren even groot zijn (een gebalanceerd ontwerp), dus dit is de enige situatie waarvoor we tweewegs-variantieanalyse met de hand zullen uitvoeren.
Omdat we voor de berekening van de kwadratensommen zowel de totalen nodig hebben voor de groepen op elk van beide factoren apart als voor de subgroepen die gevormd worden door de combinaties van beide fatcoren tegelijk, is het handig om de datamatrix als een soort kruistabel weer te geven met de ene factor als rijen en de andere als kolommen. We voegen de kwadraten van de oorspronkelijke scores toe, net als bij eenwegs-variantieanalyse. Voor het voorbeeld uit het boek (p. 263), levert dit onderstaande tabel op. NB de gemiddelden zijn niet strikt noodzakelijk maar wel erg handig om de resultaten te interpreteren.

Factor B \ Factor A	Jongens (X1)	x12	Meisjes (X2)	x22	Som nivo Factor B (ΣB)j	Som kwadraten (ΣX)j
SES Laag	2	4	4	16
	4	16	1	1
	6	36	2	4
	5	25	2	4
	5	25	3	9
Som	22	106	12	34	34	140
Gemiddelde	4,4		2,4		3,4
SES Midden	6	36	5	25
	4	16	3	9
	7	49	5	25
	4	16	3	9
	7	49	7	49
Som	28	166	23	117	51	283
Gemiddelde	5,6		4,6		5,1
SES Hoog	5	25	9	81
	6	36	6	36
	4	16	8	64
	3	9	7	49
	6	36	9	81
Som	24	122	39	311	63	433
Gemiddelde	4,8		7,8		6,3
Totaal (ΣAi en ΣXi2	74	394	74	462	148	856

Met deze getallen kunnen we de formules invullen voor de kwadratensommen, waarbij we de kwadratensom van het interactie-effect bepalen als het verschil tussen de totale en de overige kwadratensommen.
De formule van de totale kwadratensom is hetzelfde als bij de eenwegs-variantieanalyse. We hebben dus de som van alle gekwadrateerde scores nodig (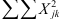, linker deel van de formule) en de totale som van de oorspronkelijke scores ( 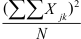in de noemer van het rechter deel van de formule).

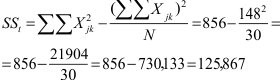
De kwadratensommen voor de hoofdeffecten worden ook hetzelfde berekend als bij eenwegs-variantieanalyse, waarbij we de sommen (totaalscores) per niveau (groep) van de factor gebruiken. De rechter term van de formules kennen we al omdat die hetzelfde is als in de formule voor de totale kwadratensom.

Voor Factor A (geslacht) wordt de kwadratensom:

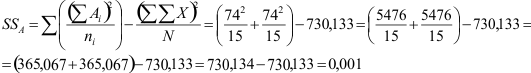
Aangezien jongens en meisjes dezelfde gemiddelden hebben, hadden we eigenlijk kunnen weten dat de kwadratensom 0 is. Het piepkleine getal dat we overhouden komt door tussentijdse afronding.

Voor Factor B (SES) wordt de kwadratensom:

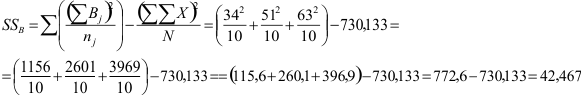
Voor de binnengroepenkwadratensom hebben we de som van alle kwadraten (linker term van de formule) weer nodig, die we ook al nodig hadden voor de totale kwadratensom, en de som van de scores per subgroep (in de noemer van de rechter term van de formule). We kunnen deze getallen aflezen uit de tabel. Voor elke subgroep krijgen we dus een breuk in de rechter term van de formule.

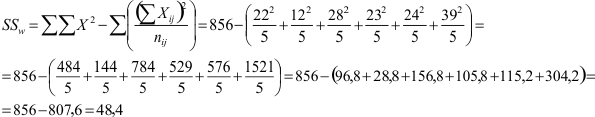
We kunnen nu de samenvattende tabel invullen.

	Sum of Squares	df	Mean Square	F
Hoofdeffecten
Sekse (A)	(SSA) 0,001	(I - 1 = 2 - 1) 1	(0,001 / 2) 0,001	(0,001 / 2,017) 0,000
SES (B)	(SSB) 42,467	(J - 1 = 3 - 1) 2	(42,467 / 2) 21,234	(21,234 / 2,017) 10,528
Interactie-effect
Sekse met SES	(SSAxB = SSt - (SSA) + SSB) + SSw) = 125,867 - (0,001 + 42,467 + 48,4) = 125,867 - 90,868) 34,999	((I - 1)(J - 1) = 1 x 2) 2	(34,999 / 2) 17,500	(17,500 / 2,017) 8,676
Binnengroepen (fout)	(SSw) 48,4	(N - J = 30 - 6) 24	(48,4 / 24) 2,017
Totaal	(SSt) 125,867	(N - 1 = 30 - 1) 29

We kunnen nu op de gebruikelijke manier nagaan of de F-waarden van de steekproef significant zijn door deze te vergelijken met de bijbehorende kritieke F-waarden.

Meervoudige vergelijkingen voeren we uit voor hoofdeffecten (niet voor interactie-effecten) en alleen wanneer er meer dan twee groepen zijn. Voer dan voor elk paar van groepen een t-toets op twee gemiddelden uit, waarbij je voor elke afzonderlijke toets het oorspronkelijke significantieniveau (bijvoorbeeld 5%) deelt door het totaal aantal t-toetsen (paren) dat je uitvoert. Kies in de significantietabel het dichtstbijzijnde significantieniveau.

Meervoudige regressieanalyse

We gebruiken regressieanalyse wanneer we één kwantitatieve (interval of ratio meetniveau) afhankelijke variabele hebben en een of meer onafhankelijke variabelen. We noemen een regressieanalyse meervoudig wanneer er minstens twee onafhankelijke variabelen zijn. Een regressieanalyse met maar één onafhankelijke variabele is een enkelvoudige regressieanalyse.
Minstens een van de onafhankelijke variabelen is numeriek, anders kunnen we beter een meerwegs-variantieanalyse uitvoeren.

Statistische nulhypothesen

1. De nulhypothese bij de toets op het hele regressiemodel: met het regressiemodel kun je in de populatie geen variantie in de afhankelijke variabele voorspellen oftewel in de populatie is de multipele correlatiecoëfficiënt nul.
   H₀: ρ_Y.1..k = 0.
2. Een nulhypothese bij elke regressiecoëfficiënt: de populatiewaarde van de regressiecoëfficiënt is nul. Maak duidelijk om welke onafhankelijke variabele (predictor) het gaat, bijvoorbeeld in een subschrift.
   Voorbeeld: H₀: β_leeftijd = 0.

Voorwaarden

De tekst van Van Peet specificeert maar liefst 8 voorwaarden, waarvan we alleen de belangrijkste drie controleren.

1. Meetniveau: de afhankelijke variabele moet minstens interval meetniveau hebben. De onafhankelijke variabelen hebben ook minstens interval meetniveau of ze zijn dichotomieën: 0/1 variabelen of -1/1 variabelen.
2. Het verband tussen de afhankelijke variabele en elke onafhankelijke (kwantitatieve) variabele is linear (rechtlijnig).
   Maak een spreidingsdiagram voor elk paar afhankelijke - onafhankelijke variabelen en ga na of de puntenwolk niet duidelijk krom is. Eigenlijk moet het verband lineair zijn wanneer je controleert voor de overige variabelen, maar dat voert hier te ver.
3. Residuen: zijn normaal verdeeld en homoscedastisch. Wanneer de variabelen niet normaal verdeeld zijn, bijvoorbeeld omdat er extreme waarden zijn, krijg je residuen die niet normaal verdeeld zijn en/of die niet voor elke voorspelde waarde van de afhankelijke variabele evenveel spreiding hebben. Als dat het geval is, zijn de berekende overschrijdingskansen niet helemaal te vertrouwen.
   We controleren dit alleen op het oog (met 2 grafieken) en we zullen alleen een waarschuwing geven in de interpretatie van de resultaten wanneer deze voorwaarden geschonden lijken te zijn. Preciezere toetsen voor de schending van deze voorwaarden en technieken om te corrigeren voor schending van deze voorwaarden gaan te ver voor de cursus IS. We troosten ons met de gedachte dat de lineaire regressieanalyse niet zo gevoelig is voor schending van deze voorwaarde.

SPSS commando

• Om een regressie uit te voeren kies je: ANALYZE – REGRESSION – LINEAR.
• Selecteer de afhankelijke variabele en plaats deze in de lijst Dependent. Selecteer de onafhankelijke variabelen en plaats deze in de lijst Independent(s). Hiermee wordt de standaard OLS-regressie uitgevoerd die jullie in deze cursus leren.
• Met ENTER worden alle onafhankelijke variabelen tegelijk in de analyse gestopt. Dit is de methode die wij aanbevelen. Normaliter voeg je alle onafhankelijke variabelen in één keer toe, maar je kunt ze ook in groepen ('blokken') toevoegen. Dan moet je de eerste groep onafhankelijke variabelen kopiëren naar het vak onder 'Independent(s):', vervolgens op de knop 'Next' klikken en de volgende groep onafhankelijke variabelen naar het vak onder 'Independent(s):' kopiëren (enzovoort).
  Wanneer je echter veel onafhankelijke variabelen hebt waarvan je niet weet of ze de afhankelijke variabelen kunnen voorspellen, kun je een van de andere methoden gebruiken. Je kunt dan bijvoorbeeld een stapsgewijze regressianalyse uitvoeren door in het vakje naast METHOD: een andere optie te kiezen dan ENTER.
• Wanneer je de regressieanalyse niet wilt uitvoeren op alle respondenten maar op één groep van respondenten, dan kun je de groepsvariabele onder SELECTION VARIABLE: zetten en via de knop RULE aangeven welke score(s) de respondenten op deze variabele 1 moeten hebben.
• Klik op de knop STATISTICS. In dit scherm kunnen extra statistische maten worden opgevraagd die vooral van belang zijn als je bepaalde assumpties moet controleren.
  Kies hier onder 'Regression coëfficiënt' voor ESTIMATES en CONFIDENCE INTERVALS. Vink verder MODEL FIT en DECRIPTIVES aan. Wanneer je een regressie doet waarin de variabelen in verschillende stappen aan het model worden toegevoegd, vink je ook R SQUARED CHANGE aan.
• Bij het submenu PLOTS zet je z_residu onder Y: en z_pred onder X:. Dit commando maakt de grafiek waarmee je de homoscedasticiteit kunt controleren. Vink ook HISTOGRAM aan om een histogram te krijgen van de residuen.
• Klik eventueel nog op de knop OPTIONS. In het betreffende scherm kun je kiezen tussen het listwise of pairwise verwijderen van missende data.

Wanneer je onafhankelijke categorische variabele wilt opnemen (zie de hint over regressieanalyses), moet je eerst nieuwe variabelen maken in SPSS voordat je de regressieanalyse uitvoert.

• Een categorische variabele moet je omzetten in één of meer dummyvariabelen: voor elke categorie minus één is een dummyvariabele nodig.
• Met TRANSFORM – RECODE INTO DIFFERENT VARIABLES maak je een dummyvariabele door één categorie van de oorspronkelijke variabele te kiezen en die de waarde 1 te geven in de nieuwe variabele. Geef alle andere categorieën een 0 op deze dummyvariabele (daarvoor is de optie ALL OTHER VALUES handig in het dialoogscherm waarin je de hercoderingen kunt opgeven). Geef de naam van de categorie die een 1 krijgt op als label voor de dummyvariabele.
• Bijvoorbeeld: voor een variabele Opleiding met als waarden 1 (laag), 2 (midden) en 3 (hoog), maak je twee dummyvariabelen, respectievelijk OplMidden (waarden 1 = wel, 0 = niet) en OplHoog (waarden 1 = wel, 0 = niet). De laatste categorie (lage opleiding) is hier de vergelijkingscategorie waarvoor geen aparte dummyvariabele nodig is.
• Let op: wanneer je toch voor elke categorie een dummyvariabele maakt, slaat de regressieanalyse op tilt.

SPSS Output

In dit voorbeeld hebben we een regressieanalyse uitgevoerd waarbij we stap voor stap predictoren laten toevoegen aan het model (methode FORWARD).
De belangrijkste resultaten staan in de volgende tabellen.

Model Summarye
Model	R	R Square	Adjusted R Square	Std. Error of the Estimate	Change Statistics
					R Square Change	F Change	df1	df2	Sig. F Change
1	,362a	,131	,130	1,231	,131	232,496	1	1544	,000
2	,451b	,204	,203	1,179	,073	141,103	1	1543	,000
3	,500c	,250	,249	1,144	,046	95,492	1	1542	,000
4	,504d	,254	,252	1,142	,004	8,588	1	1541	,003
a. Predictors: (Constant), Hoe oud bent u?
b. Predictors: (Constant), Hoe oud bent u?, Bent u een man?
c. Predictors: (Constant), Hoe oud bent u?, Bent u een man?, Politiek wantrouwen
d. Predictors: (Constant), Hoe oud bent u?, Bent u een man?, Politiek wantrouwen, Hoe vaak gebruikt u internet?
e. Dependent Variable: Hoe vaak leest u de krant?

De eerste tabel geeft aan hoe goed de afhankelijke variabele voorspeld kan worden: het percentage verklaarde variantie van de afhankelijke variabele (R²). Voor elk model wordt R² gegeven, die oploopt van 0,13 (Model 1) tot 0,254 (Model 4). Dit zegt echter weinig want het toevoegen van een extra onafhankelijke variabele levert altijd een verhoging van R² op.
Daarom kijken we of de verhoging van R² bij toevoeging van een extra predictor significant is: mogen we ervan uitgaan dat het model met de extra predictor ook in de populatie meer voorspelt? De nulhypothese is dat R² in de populatie niet toeneemt. De F-toets op deze nulhypothese staat in de meest rechtse kolommen van de tabel. We zien dat F telkens zeer significant is (p is steeds kleiner dan 0,01) dus mogen we ervan uitgaan dat alle extra predictoren een bijdrage leveren aan de voorspelling van de frequentie waarmee men de krant leest in de populatie van alle Nederlanders.
Kortom, we kiezen voor Model 4 als beste model, dat naar schatting 25% verklaard van de verschillen tussen Nederlanders wat betreft de frequentie dat ze de krant lezen.

ANOVAe
Model		Sum of Squares	df	Mean Square	F	Sig.
1	Regression	352,454	1	352,454	232,496	,000a
	Residual	2340,643	1544	1,516
	Total	2693,097	1545
2	Regression	548,565	2	274,283	197,347	,000b
	Residual	2144,532	1543	1,390
	Total	2693,097	1545
3	Regression	673,626	3	224,542	171,453	,000c
	Residual	2019,471	1542	1,310
	Total	2693,097	1545
4	Regression	684,818	4	171,204	131,369	,000d
	Residual	2008,279	1541	1,303
	Total	2693,097	1545
a. Predictors: (Constant), Hoe oud bent u?
b. Predictors: (Constant), Hoe oud bent u?, Bent u een man?
c. Predictors: (Constant), Hoe oud bent u?, Bent u een man?, Politiek wantrouwen
d. Predictors: (Constant), Hoe oud bent u?, Bent u een man?, Politiek wantrouwen, Hoe vaak gebruikt u internet?
e. Dependent Variable: Hoe vaak leest u de krant?

De tweede tabel geeft de F-toets op het regressiemodel. De nulhypothese is dat het regressiemodel in de populatie de afhankelijke variabele niet voorspelt. Dit betekent dat de multipele correlatiecoëfficiënt in de populatie nul is (H₀ : ρ_Y.12...k = 0) of dat alle hellingen in de populatie nul zijn (H₀ : β₁ = β₂ = … = β_k = 0).
Een significant resultaat betekent dus dat we de nulhypothese verwerpen. We kunnen met de gebruikte onafhankelijke variabelen dus de scores op de afhankelijke variabelen enigszins voorspellen, ook in de populatie. In feite wisten we dit al op grond van de F-toetsen op de verandering van R². Bij Model 4 krijgen we nu echter de F-toets voor het hele model met de 4 predictoren tegelijk. Dit is de waarde die we in de interpretatie vermelden.

Coefficientsa
Model		Unstandardized Coefficients		Standardized Coefficients	t	Sig.	95,0% Confidence Interval for B
		B	Std. Error	Beta			Lower Bound	Upper Bound
1	(Constant)	3,270	,077		42,655	,000	3,119	3,420
	Hoe oud bent u?	,030	,002	,362	15,248	,000	,026	,033
2	(Constant)	2,986	,077		38,699	,000	2,835	3,138
	Hoe oud bent u?	,028	,002	,338	14,843	,000	,024	,031
	Bent u een man?	,715	,060	,271	11,879	,000	,597	,833
3	(Constant)	3,958	,124		31,798	,000	3,714	4,202
	Hoe oud bent u?	,028	,002	,337	15,243	,000	,024	,031
	Bent u een man?	,735	,058	,279	12,576	,000	,621	,850
	Politiek wantrouwen	-,038	,004	-,216	-9,772	,000	-,046	-,030
4	(Constant)	3,460	,210		16,440	,000	3,047	3,873
	Hoe oud bent u?	,031	,002	,379	14,445	,000	,027	,035
	Bent u een man?	,712	,059	,270	12,103	,000	,597	,828
	Politiek wantrouwen	-,037	,004	-,207	-9,331	,000	-,044	-,029
	Hoe vaak gebruikt u internet?	,072	,025	,077	2,930	,003	,024	,120
a. Dependent Variable: Hoe vaak leest u de krant?

De derde tabel geeft de resultaten voor de onderdelen van de regressievergelijking: de schatting van het intercept (aangegeven met ‘Constant’) en de schattingen van de hellingen voor de onafhankelijke variabelen. Omdat we een stapsgewijze regressie hebben gedaan, krijgen we de schattingen voor alle modellen apart. Rapporteer alleen de schattingen uit het model dat je uiteindelijk gekozen hebt.
Eerst wordt de ongestandaardiseerde waarde gegeven (onder B) met de standaardfout. Dit is dus de waarde die via een t-toets op overschrijdingskans wordt getoetst (de kolommen t en Sig.) met als nulhypothese telkens dat het intercept of de helling nul is in de populatie.
Onder Standardized Coefficients (Beta) wordt tenslotte de helling gegeven voor gestandaardiseerde variabelen (b^*). Hoeveel standaardafwijkingen verandert de voorspelde waarde van de afhankelijke variabele wanneer de onafhankelijke variabele 1 standaardafwijking groter is?Hiermee kun je de effecten van verschillende (continu verdeelde) onafhankelijke variabelen met elkaar vergelijken binnen een analyse: hoe hoger de absolute waarde van b^*, des te sterker is het effect. In een enkelvoudige regressieanalyse kan de sterkte van het verband b* kan op dezelfde wijze geïnterpreteerd worden als r: 0,10 = klein/zwak, 0,30 = middelgroot/middelmatig en 0,50 = groot/sterk. Maar dit geldt niet voor een meervoudige regressie, waar b^* zelfs groter dan 1 en kleiner dan -1 kan zijn, wat natuurlijk niet mogelijk is bij de correlatiecoefficient r.
Zowel bij de ongestandaardiseerde als de gestandaardiseerde regressiecoëfficiënten (regressiegewichten) gaat het om partiële effecten, dat wil zeggen effecten waarbij de mogelijke invloeden van de andere onafhankelijke variabelen in het model zijn uitgeschakeld. Je kunt dus zeggen dat dit de effecten zijn bovenop mogelijke effecten van andere onafhankelijke variabelen.

Wanneer je de gestandaardiseerde regressiecoëfficiënten van een predictor vergelijkt voor de vier modellen, zie je dat er weinig verandert. In dit voorbeeld leidt de toevoeging van een extra onafhankelijke variabele niet tot de sterke wijziging van het effect van andere onafhankelijke variabelen.

De onafhankelijke variabele Sekse is hier een dummyvariabele met waarde 1 voor mannen en waarde 0 voor vrouwen. De ongestandaardiseerde regressiecoëfficiënt betekent hier dat mannen gemiddeld 0,71 minder vaak de krant lezen dan vrouwen.
De frequentie van het krantenlezen bij vrouwen wordt voorspeld met de regressievergelijking:

KrantLezen = 3,460 + 0,031 * Leeftijd + 0,712 * Man = 3,460 + 0,031 * Leeftijd + 0,712 * 0 = 3,460 + 0,031 * Leeftijd

Let op, vrouwen hebben de score 0 op de dummyvariabele Man, dus de laatste term valt weg uit de regressievergelijking.
Voor mannen is de regressievergelijking:

KrantLezen = 3,460 + 0,031 * Leeftijd + 0,712 * Man = 3,460 + 0,031 * Leeftijd + 0,712 * 1 = 3,460 + 0,031 * Leeftijd + 0,712

Omdat mannen de score 1 hebben op de dummyvariabele Man, krijgt hun voorspelde leesfrequentie van kranten er standaard 0,712 bij. Dit is dus het geschatte gemiddelde verschil tussen vrouwen en mannen.

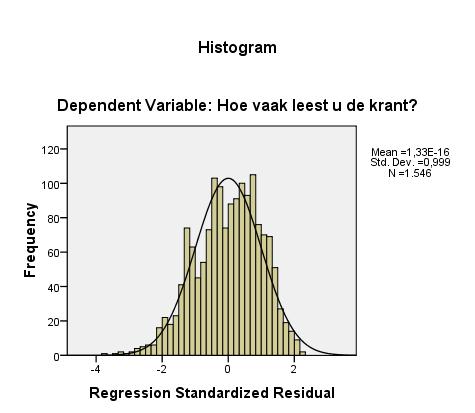
De grafieken waarmee we de veronderstellingen over de residuen controleren, staan hieronder. De residuen lijken normaal verdeeld te zijn, al is de rechter staart wat kort, zodat de verdeling van de residuen wat scheef is. Vermoedelijk komt dit hier door een wat scheve verdeling van de afhankelijke variabele.
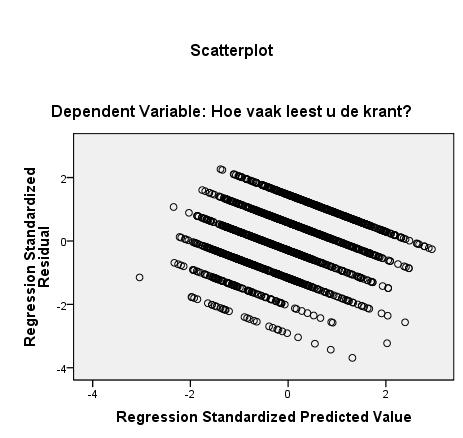
De grafiek van de gestandaardiseerde residuen tegen de gestandaardiseerde voorspelde waarden laat zien dat de residuen overal ongeveer evenveel verspreid zijn (de vertikale doorsnede van de puntenwolk is overal ongeveer even groot) al zakt de wolk naar rechts toe wel weg. Dit laatste betekent dat bij hogere voorspelde waarden de residuen gemiddeld negatiever worden: de voorspelling zit wat te hoog. Dit wijst op een vermoedelijk niet helemaal rechtlijnig verband tussen de variabelen.
Het feit dat de residuen op gescheiden lijnen liggen is het gevolg van de meting van leesfrequentie met gehele getallen. De veronderstelling dat leesfrequentie continu verdeeld is in de populatie gaat niet op: frequenties zijn nu eenmaal gehele getallen. De resultaten van de regressieanalyse worden daar echter meestal niet door beïnvloed.

Rapportage

Vermeld het volgende:

• De waarde van de toetsingsgrootheid, het aantal vrijheidsgraden en de overschrijdingskans van het regressiemodel.
• Als er een significant model is, de effectgrootte (R²).
• Als er een significant model is, de ongestandaardiseerde regressiecoefficiënten (met het teken b en het 95% betrouwbaarheidsinterval) of gestandaardiseerde regressiecoefficiënten (met het teken b*), de t-waarde en overschrijdingskans van deze coëfficiënten.
• Maak duidelijk wat de eenheden en variabelen in het onderzoek zijn.
• Vermeld het wanneer de residuen duidelijk niet normaal verdeeld zijn en duidelijk niet wijzen op homoscedasticiteit.

Rekenen voor reguliere studenten

Reguliere studenten hoeven alleen ontbrekende getallen in SPSS output te kunnen aanvullen en geschatte waarden uit te rekenen op grond van een regressievergelijking.

Wanneer minstens twee van de drie kwadratensommen (SS_Y , SS_regressie , SS_residu) gegeven zijn, moet je zowel de F-toets op het hele regressiemodel kunnen uitrekenen als de daarbij horende determinatiecoëfficiënt R² en multipele correlatiecoëfficiënt R. Onderstaande tabellen laten zien hoe je die berekeningen uitvoert. De formules staan ook op het formuleblad.

ANOVAe
	Sum of Squares	df	Mean Square	F	Sig.
Regression	= SSY - SSresidu	k	SSregressie / k	MSregressie / MSresidu	zoek op in de tabel
Residual	= SSY - SSregressie	N - k - 1	SSresidu / (N - k - 1)
Total	= SSregressie + SSresidu	N - 1

R2	SSregressie / SSY
R	√(R2)

Let op, de kwadratensom van de afhankelijke variabele (SS_Y) kun je gemakkelijk afleiden uit de variantie of standaarddeviatie van de afhankelijke variabele. Deze kwadratensom is immers de teller in de formule voor de variantie. Vermenigvuldig dus de geschatte variantie van de variabele met N – 1 (het aantal waarnemingen min 1) om deze kwadratensom te krijgen.

Bij de regressiecoëfficiënt moet je de t-waarde en het betrouwbaarheidsinterval kunnen uitrekenen wanneer de standaardfout van de regressiecoëfficiënt gegeven is. Wanneer de standaarddeviatie van de afhankelijke en van de onafhankelijke variabele bekend is, moet je de gestandaardiseerde regressiecoëfficiënt (b*) kunnen uitrekenen.

Coefficientsa
	Unstandardized Coefficients		Standardized Coefficients	t	Sig.	95,0% Confidence Interval for B
	B	Std. Error	Beta			Lower Bound	Upper Bound
Hoe oud bent u?	bi	sbi	bi ∙ (si / sY)	(bi - β0) / sbi	opzoeken in de tabel	bi - tkrit ∙ sbi	bi + tkrit ∙ sbi

Tenslotte moet je voorspelde waarden kunnen uitrekenen wanneer de (ongestandaardiseerde) regressiecoëfficiënten en de constante gegeven zijn.

Rekenen voor excellentiegroep

Berekenen van de enkelvoudige regressievergelijking

Bij BS heb je geleerd hoe je de constante (α) en de regressiecoëfficiënt (b) kunt berekenen in een enkelvoudige regressieanalyse. We hebben nu een rekenformule voor de regressiecoëfficiënt, die de berekeningen iets eenvoudiger maakt: je hoeft alleen de producten van de onafhankelijke en de afhankelijke variabele (XY) toe te voegen aan de datamatrix en de kwadraten van de onafhankelijke variabele (X²).

	x	y	xy	x2
	1	8	8	1
	1	10	10	1
	2	6	12	4
	3	7	21	9
	3	6	18	9
	3	5	15	9
	4	6	24	16
	5	5	25	25
Som	22	53	133	74

We kunnen nu de formule voor b invullen:

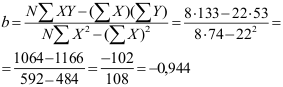
Wanneer X 1 hoger wordt, wordt de geschatte waarde van Y -0,94 lager. Er is dus een negatief effect van X op Y.
Wanneer we de correlatiecoëfficiënt weten (hier: r_XY = -0,778) en de standaardafwijking van X (hier: s_X = 1,389) en Y (hier: s_Y = 1,685), kunnen we b op een eenvoudiger manier uitrekenen:
b = r_XY ∙ s_Y / s_X = -0,778 ∙ 1,685 / 1,389 = -0,778 ∙ 1,213 = -0,944 .

Nu kunnen we a ook uitrekenen:

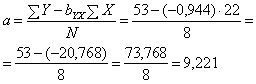
De regressievergelijking wordt dus:

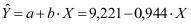
Voor een enkelvoudige regressie kan de standaardfout van de regressiecoëfficiënt berekend worden op grond van de kwadratensommen. De kwadratensommen kunnen berekend worden met behulp van het gemiddelde en de voorspelde waarden van de afhankelijke variabele. NB voor de berekening van alleen de standfout van de regressiecoëfficiënt is het voldoende om de kwadratensom van de fouten (de residuen) uit te rekenen. Wanneer je ook R of R² moet uitrekenen, moet je ook de kwadratensom van de afhankelijke variabele (Y) uitrekenen.
Dit gaat als volgt:

	x	y	ŷ	y - ŷ	(y - ŷ)2	MY	y - MY	(y - MY)2
	1	8	8,278	-0,278	0,077	6,625	1,375	1,891
	1	10	8,278	1,722	2,965	6,625	3,375	11,391
	2	6	7,333	-1,333	1,777	6,625	-0,625	0,391
	3	7	6,389	0,611	0,373	6,625	0,375	0,141
	3	6	6,389	-0,389	0,151	6,625	-0,625	0,391
	3	5	6,389	-1,389	1,929	6,625	-1,625	2,641
	4	6	5,444	0,556	0,309	6,625	-0,625	0,391
	5	5	4,500	0,500	0,250	6,625	-1,625	2,641
Som	22	53		0	7,831		0	19,878
Gemiddeld		6,625

De totale kwadratensom: SS_Y = Σ(Y - M_Y)² = 19,878 .
De kwadratensom van de fouten (residuen): SS_residu = Σ(Y - Ŷ)² = 7,831 .
De kwadratensom van de regressie is dan: SS_regressie = SS_Y - SS_residu = 19,878 - 7,831 = 12,047 .
Tenslotte hebben we ook de kwadratensom van de onafhankelijke variabele nodig, waarvoor de benodigde deelresultaten al in de eesrte tabel berekend zijn:

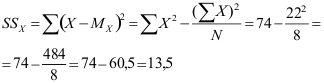
Nu kan de standaardfout van de regressiecoëfficiënt uitgrekend worden: